Maybe you use MMUULT() for a specific purpose (perhaps nested within another function) and somehow utilize a 'scalar' result.MMULT in its essnce is not a C-S-E formula, it multiplies n columns by n rows and retunrs a scalar.
What is the issue you are referring to?
But, by definition 1 Matrix Multiplying another matrix will virtually alway yield another matrix.
Moreover, give some matrix A and another matrix B, if the two are multiplicatively conformable, then their product is a matrix, let's call it C, whose elements are linear combinations of the rows of A with the columns of B.
In order for two matrices to be considered multiplicatively conformable the number of columns in the first matrix must = the number of rows in the second.
That is if A is a m x n matrix and B is a p x q matrix, then A and B are multiplicatively conformable iff n = p.
The resultant matrix C will have dimensions m x q.
So this last point is important when utilizing MMULT() You must pre-determine the resultant matrix's dimensions in order to execute MMULT properly.
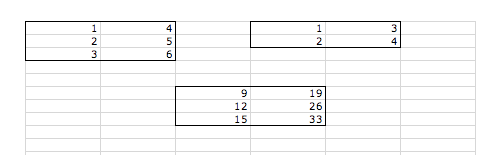
Example below: The top-left matrix is dimensions: 3 x 2 and the top-right is 2 x 2
Therefore, in order to get the resultant (bottom) matrix, you must highlight a 3 x 2 range before entering MMULT(Array1, Array2) and then press C-S-E.
There are 3 wrong ways to use MMULT() and they all result in the same answer:
If you do not highlight the result matrix's range and press either 'Enter' or 'C-S-E' it will return ONLY the first element of the resultant array.
If you do highlight the result matrix's range BUT do not press 'C-S-E' the 1st element of the resultant will be returned.
You dig? Or am I just telling you stuff you already know?
P.S. Did you mean to answer Question 5 and it was cut off? Or is it still up in the air?








 Reply With Quote
Reply With Quote